Докажите что при любых целых a 1)a³+2a²+3a либо делится на 4, либо при делении на 4 даёт остаток 2 2)2a³+a²+5a либо делится на 3, либо при делении на 3 даёт остаток 2
допустим что стороны прямоугольника A и B, и площадь S. Тогда S=A*B (площадь равно произведению сторон). Далее сказано, что одна сторона больше другой на 11 см. доопустим A=B+11. следовательно можно составить уравнение: S=(B+11)*B. Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение:
Далее решаем как обычное квадратное уравнение. В итоге получим что . Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
Квадратное уравнение имеет единственный корень, когда дискрименант равен нулю: D=0 (a+3)x²+(a+4)x+2=0 a=? D=0=(-(a+4))²-4×(a+3)×2 (a+4)²-8(a+3)=0 a²+8a+16-8a-24=0 a²-8=0 a²=8 a1=-√8 a2=√8 При а=-√8 и а=√8, кв.уравнение имеет 1 корень.
допустим что стороны прямоугольника A и B, и площадь S. Тогда S=A*B (площадь равно произведению сторон). Далее сказано, что одна сторона больше другой на 11 см. доопустим A=B+11. следовательно можно составить уравнение: S=(B+11)*B.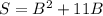 Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение:
Далее у нас сказано, что площадь равна 60 см(в квадрате). Следовательно составляем квадратное уравнение: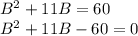
Далее решаем как обычное квадратное уравнение. В итоге получим что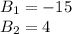 . Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
. Меньше нуля быть не может, поэтому B=4. А т.к. А=B+11, то А=4+11=15.
А=15
и B=4.
Периметр будет равен (A+B)*2=(15+4)*2=19*2=38см.
(a+3)x²+(a+4)x+2=0
a=?
D=0=(-(a+4))²-4×(a+3)×2
(a+4)²-8(a+3)=0
a²+8a+16-8a-24=0
a²-8=0
a²=8
a1=-√8
a2=√8
При а=-√8 и а=√8, кв.уравнение имеет 1 корень.
проверка:
a=-√8
(-√8+3)х²+(-√8+4)х+2=0
(-2,8284+3)х²+(-2,8284+4)х+2=0
0,1716x²+1,1716x+2=0
D=(-1,1716)²-4×0,1716×2=1,3726-1,3728=-0,0002~0
x=-1,1716/2×0,1716=-3,41375~-3,414
a=√8
(√8+3)x²+(√8+4)x+2=0
(2,8284+3)x²+(2,8284+4)x+2=0
5,8284x²+6,8284x+2=0
D=(-6,8284)²-4×5,8284×2=46,627-46,6272=-0,0002~0
x=-6,8284/2×5,8284=-0,58578~-0,586