Войти
Регистрация
Спроси ai-bota
В
Все
Б
Биология
Б
Беларуская мова
У
Українська мова
А
Алгебра
Р
Русский язык
О
ОБЖ
И
История
Ф
Физика
Қ
Қазақ тiлi
О
Окружающий мир
Э
Экономика
Н
Немецкий язык
Х
Химия
П
Право
П
Психология
Д
Другие предметы
Л
Литература
Г
География
Ф
Французский язык
М
Математика
М
Музыка
А
Английский язык
М
МХК
У
Українська література
И
Информатика
О
Обществознание
Г
Геометрия
Показать больше
Показать меньше
kri2221
04.02.2023 14:20 •
Алгебра
Доказать, что n! не делится на 2^n (n>=1)
Показать ответ
Ответ:
Nastysha222
15.10.2020 15:42
Сравним степени вхождения двойки в
и
. В первом случае, очевидно,
. Во втором:
. Поэтому
0,0
(0 оценок)
Популярные вопросы: Алгебра
karolinaskinger
16.11.2020 11:23
Найдите область определения функции: у= под корнем х+3 - под корнем 7-2х надо! решите , буду...
fonaut21krit
30.05.2023 10:18
При каких значениях параметра корни уравнения x²+(2a+1)x+a²-4a+3=0 являются положительными числами?...
marta12t
01.05.2023 08:13
Как вычислить sin (-1560градусов) ?...
Jinx2002
20.06.2020 10:39
Каждому из четырёх чисел в левом столбце соответствует отрезок, которому оно принадлежит. установите соответствие между числами и отрезками из правого столбца....
Lisaaaaakot
12.02.2021 23:29
4x-1рівність -2 1.3...
MorozilkAAA
26.08.2022 08:04
Установите соответствие....
masenkon524
16.01.2022 00:56
Решите уравнение графическим ...
ankateren
26.04.2023 07:52
1) а, если а .= -3 и d = 2;2) а, если а = 2,3 и d = 1,2;3) а, если аесли а = -2,1 и d = -2,3;4) а, если а 0,6 и d = 1,02.1...
lebedevan189
23.03.2023 13:51
Зделайте Найдите значение функции, заданной формулой y=3x+2 для значений аргумента равных -4...
kilbas1ggttyi
06.07.2021 03:40
Упрости алгебраическую сумму многочленов: (20410a−29a2)+(19a2−1410a) ....
Полный доступ
Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota
Оформи подписку
О НАС
О нас
Блог
Карьера
Условия пользования
Авторское право
Политика конфиденциальности
Политика использования файлов cookie
Предпочтения cookie-файлов
СООБЩЕСТВО
Сообщество
Для школ
Родителям
Кодекс чести
Правила сообщества
Insights
Стань помощником
ПОМОЩЬ
Зарегистрируйся
Центр помощи
Центр безопасности
Договор о конфиденциальности полученной информации
App
Начни делиться знаниями
Вход
Регистрация
Что ты хочешь узнать?
Спроси ai-бота
Сравним степени вхождения двойки в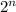 и
и 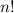 . В первом случае, очевидно,
. В первом случае, очевидно, 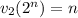 . Во втором:
. Во втором: ![v_{2}(n!)=\sum\limits_{i=1}^{\infty}[\frac{n}{2^{i}}]< \sum\limits_{i=1}^{\infty}\frac{n}{2^{i}}=n](/tpl/images/1358/9881/79b0f.png) . Поэтому
. Поэтому