Выполнить построение графиков, взяв в качестве двух опорных точек случайное значение аргумента, посчитать значение функций. Таким образом отложить в системе координат две точки для каждого графика и соединить их проходящей через них прямой. Графики пересекутся, найти точку пересечения и записать ее координаты
Но этот метод не оптимален, так как получится значение в 2.9 см, что и мерить то будет неудобно. Можно его нарисовать, не повредит, но мы будем делать упор на 2-й путь
2-й
Приравняем функции, необходимо решить линейное уравнение, найдя значение аргумента x, которое будет равно для двух функций:
y = y
0.3x + 2 = x - 0.1
0.3x + 2.1 = x
x - 0.3x = 2.1
0.7x = 2.1
x = = 3
Подставим значение аргумента в любую из двух функций, чтобы найти значение y, наиболее удобной будет вторая:
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях
Да, пересекаются
Точка пересечения графиков - (3, 2.9)
Объяснение:
Найти точку пересечения можно двумя путями
1-й
Выполнить построение графиков, взяв в качестве двух опорных точек случайное значение аргумента, посчитать значение функций. Таким образом отложить в системе координат две точки для каждого графика и соединить их проходящей через них прямой. Графики пересекутся, найти точку пересечения и записать ее координаты
Но этот метод не оптимален, так как получится значение в 2.9 см, что и мерить то будет неудобно. Можно его нарисовать, не повредит, но мы будем делать упор на 2-й путь
2-й
Приравняем функции, необходимо решить линейное уравнение, найдя значение аргумента x, которое будет равно для двух функций:
y = y
0.3x + 2 = x - 0.1
0.3x + 2.1 = x
x - 0.3x = 2.1
0.7x = 2.1
x =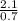 = 3
= 3
Подставим значение аргумента в любую из двух функций, чтобы найти значение y, наиболее удобной будет вторая:
y = x - 0.1
y = 3 - 0.1
y = 2.9
Или:
y = 0.3x +2
y = 0.3 * 3 + 2 = 0.9 + 2
y = 2.9
Что и требовалось доказать
Многие задаются вопросами: зачем нужна тригонометрия? Как она используется в нашем мире? С чем может быть связана тригонометрия? И вот ответы на эти вопросы. Тригонометрия или тригонометрические функции используются в астрономии (особенно для расчётов положения небесных объектов), когда требуется сферическая тригонометрия, в морской и воздушной навигации, в теории музыки, в акустике, в оптике, в анализе финансовых рынков, в электронике, в теории вероятности, в статистике, в биологии, в медицинской визуализации ,например, компьютерной томографии и ультразвук, в аптеках, в химии, в теории чисел, в сейсмологии, в метеорологии, в океанографии, во многих физических науках, в межевании и геодезии, в архитектуре, в фонетике, в экономике, в электротехнике, в машиностроении, в гражданском строительстве, в компьютерной графике, в картографии, в кристаллографии, в разработке игр и многих других областях