Это система уравнений. ее решение сводится к тому, чтоб из одного уравнения в системе найти значение х или у, и подставив это значение во второе уравнение, решить его. в таких системах, для удобства, надо умножить первое и второе уравнение на такие числа, чтоб х или у в первом и во втором уравнении стали одинаковыми. например, если мы первое уравнение умножим на2, а второе на 5, то получим 2*4х-2*5у=2*10 5*3х+5*2у=5*19
8х-10у=20 15х+10у=95
-10у и 10у при этом сокращаются. остаётся: 8х+15х=20+95 23х=115 х=5 подставляя значение х в любое уравнение, находим у: 4*5-5у=10 -5у=-10 5у=10 у=2
Так как 2 > π/2 ≈ 1,57, то есть 2∉[-π/2; π/2] , то нельзя сразу воспользоваться формулой arcsin (sin α) = α. Нужно преобразовать выражение с формул приведения.
arcsin (sin 2) = arcsin (sin (π - 2)) = π - 2
После преобразования угол (π - 2) ≈1,14 ∈ [-π/2; π/2]
2*4х-2*5у=2*10
5*3х+5*2у=5*19
8х-10у=20
15х+10у=95
-10у и 10у при этом сокращаются. остаётся:
8х+15х=20+95
23х=115
х=5
подставляя значение х в любое уравнение, находим у:
4*5-5у=10
-5у=-10
5у=10
у=2
Для вычисления понадобятся следующие определения и формулы.
arcsin b = α
Арксинусом числа b∈[-1; 1] называется угол α такой, что
sin α = b и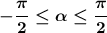 .
.
arcsin (sin α) = α, если![\boldsymbol{\alpha \in \Big[-\dfrac{\pi }{2}; \dfrac{\pi }{2}}\Big]](/tpl/images/0315/2594/4cc60.png)
sin (arcsin b) = b, где b∈[-1; 1]
cos (arcsin b) ≥ 0 и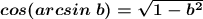 , b∈[-1; 1]
, b∈[-1; 1]
sin (2α) = 2 sin α · cos α
=====================================================
sin (2arcsin 0,75) = 2 · sin(arcsin 0,75) · cos (arcsin 0,75)
0,75∈[-1; 1] ⇒ sin(arcsin 0,75) = 0,75 = 3/4
===================================================
===================================================
arcsin (sin2)
Так как 2 > π/2 ≈ 1,57, то есть 2∉[-π/2; π/2] , то нельзя сразу воспользоваться формулой arcsin (sin α) = α. Нужно преобразовать выражение с формул приведения.
arcsin (sin 2) = arcsin (sin (π - 2)) = π - 2
После преобразования угол (π - 2) ≈1,14 ∈ [-π/2; π/2]