Для определения оптимального плана выпуска мужской обуви фиксировалась относительная частота (в процентах) размеров проданной в течение месяца обуви. найдите пропущенное значение относительной частоты.
Степень с рациональным показателем Степень с рациональным показателем. Решение примеровЛекция: Степень с рациональным показателем и её свойстваСтепень с рациональным показателемСтепень с рациональным показателем - это та, в показателе которой находится конечная обыкновенная или десятичная дробь. Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.Свойства степени с рациональным показателемВсе, перечисленные ниже степени используются для рациональных чисел p, q и для положительных a, b.1. Если Вам необходимо умножить две степени с рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.ap * aq = ap+q.Например:2. Если необходимо разделить две степени c рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть.ap / aq = ap-q .Например,3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.(ap )q = ap*qНапример,4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.(a * b)p = ap * bp5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.(a / b)p = ap / bq6. Если некоторая дробь имеет отрицательный рациональный показатель степени, то для избавления от знака минуса, её следует перевернуть.Например,Очень важно помнить, что знак степени не влияет на знак выражения при возведении в степень
Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)
Степень с рациональным показателем Степень с рациональным показателем. Решение примеровЛекция: Степень с рациональным показателем и её свойстваСтепень с рациональным показателемСтепень с рациональным показателем - это та, в показателе которой находится конечная обыкновенная или десятичная дробь. Любую степень с рациональным показателем можно представить в виде корня, чья степень будет равна знаменателю дроби, находящейся в показателе степени, а числитель будет степенью подкоренного выражения.Свойства степени с рациональным показателемВсе, перечисленные ниже степени используются для рациональных чисел p, q и для положительных a, b.1. Если Вам необходимо умножить две степени с рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели сложить.ap * aq = ap+q.Например:2. Если необходимо разделить две степени c рациональными показателями, которые имеют одинаковые основания, то в таком случае основание необходимо оставить без изменения, а показатели вычесть.ap / aq = ap-q .Например,3. Если необходимо возвести одну степень в другую, основанием результата останется то же число, а показатели степени перемножаются.(ap )q = ap*qНапример,4. Если в некоторую степень необходимо возвести произведение произвольных чисел, то можно воспользоваться неким распределительным законом, при котором получим произведение различных оснований в одной и той же степени.(a * b)p = ap * bp5. Аналогичное свойство можно применять для деления степеней, иначе говоря, для возведения обыкновенной двоби в степень.(a / b)p = ap / bq6. Если некоторая дробь имеет отрицательный рациональный показатель степени, то для избавления от знака минуса, её следует перевернуть.Например,Очень важно помнить, что знак степени не влияет на знак выражения при возведении в степень
ответ: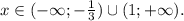
Объяснение:
-3x² + 2x +1 < 0;
3x² - 2x - 1 > 0;
Дискриминант равен 2²+4*1*3 = 4+12 = 16.
Корни трехчлена равны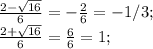
Значит 3x² - 2x - 1 = (3x+1)(x-1) > 0;
Рассмотрим значение выражения на каждом из интервалов: (-∞; -1/3); (-1/3; 1); (1; +∞). На первом из них 3х+1 < 0 и х-1 < 0. Значит произведение больше 0. На втором 3х+1 > 0 и х-1 < 0. Значит их произведение меньше 0. На третьем 3х+1 > 0 и х-1 > 0. Значит их произведение больше 0. Подходит только интервал (-∞; -1/3) и (1; +∞)