Дана функция y=f(x), где f(x)={−2x,если−10≤x≤0−13x2,если0Вычисли f(−4).

ответ: f(−4)=

F(x) = 3x^2 -x -2.
Построим квадратичную функцию. Графиком функции является парабола, ветви направлены вверх, т.к. 3>0.

Координаты вершины параболы:

x = -b/2a = 1/(2*3) = 1/6.

y=3 * (1/6)^2 - 1/6 - 2 = - 25/12

И найдем корни уравнения

D=b^2-4ac = 1 + 24 = 25

x1 = -2/3
x2 = 1

Видим, что парабола пересекает ось Ох в точке x=-2/3 и x=1

Найдем множество значений х, при которых:

а) f(x)>0
  x ∈ (-∞;-2/3)∪(1;+∞)

б) f(x)<0
   x ∈ (-2/3;1).

g(x) = -x^2 + 2x - 3

Найдем координаты вершины параболы(ветви параболы направлены вниз, т.к. -1<0)

x = -b/2a = -2/(-2) = 1

y = -1 + 2*1 - 3  = -2

(1;-2) - координаты вершины параболы.

Найдем множество значений х, при которых:

а) g(x)>0

Видим, что нет таких х

б) g(x) < 0

А здесь х - любое. Можно сделать так (x-1)²+2<0

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .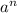

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .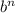

Рассмотрим многочлен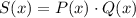 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :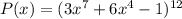

- степень определяется выражением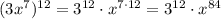 , то есть степень равна 84

- свободный член равен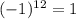

Для многочлена :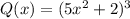

- степень определяется выражением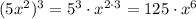 , то есть степень равна 6

- свободный член равен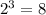

Наконец, для многочлена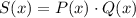 получим:

- степень определяется выражением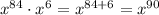 , то есть степень равна 90

- свободный член равен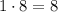

Сумма степени и свободного члена многочлена :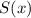

ответ: 98