Уравнение касательной к графику функции в точке :
а)
б)
Находим значения функции и производной в точке касания:
Составляем уравнение касательной:
Уравнение касательной к графику функции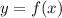 в точке
в точке 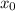 :
:
а)
б)
Находим значения функции и производной в точке касания:
Составляем уравнение касательной: