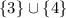Войти Регистрация Спроси ai-bota

Будет ли данное выражение 4x/11=4/11*x одночленом?

Показать ответ

Ответ:

ralibaev

29.08.2021 16:45

sin (синус) - отношение противолежащего катета к гипотенузе

cos (косинус) - отношение прилежащего катета к гипотенузе

tg (тангенс) - отношение противолежащего катета к прилежащему

ctg (котангенс) - отношение прилежащего катета к противолежащему

arcsin (арксинус) - арксинусом числа х есть значение угла А, для которого sinA=x

arccos (арккосинус) - арккосинусом числа х есть значение угла А, для которого cosA=x

arctg (арктангенс) - арктангенсом числа х есть значение угла А, для которого tgA=x

arcctg (арккотангенс) - арккотангенсом числа х есть значение угла А, для которого ctgA=x

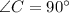
Из $\triangle$ ABC $\angle C=90^\circ$

$sin A=\frac{BC}{AB}\\cos A=\frac{AC}{AB}\\tg A=\frac{BC}{AC}\\ctg A=\frac{AC}{BC}\\arcsin \frac{BC}{AB}=\angle A\\arccos \frac{AC}{AB}=\angle A\\arctg \frac{BC}{AC}=\angle A\\arcctg \frac{AC}{BC}=\angle A$

0,0(0 оценок)

Ответ:

asadbek7703

10.08.2020 23:02

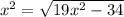
1) $x^2=\sqrt{19x^2-34}$

Область определения уравнения:

$19x^2-34 \geq 0$

$x \in (-\infty;-\sqrt{\frac{34}{19}}] \cup [\sqrt{\frac{34}{19}};+\infty)$

Возведем обе неотрицательные части в квадрат:

x^4=19x^2-34

x^4-19x^2+34=0

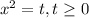
Решение подобного биквадратного уравнения сводится к замене вида: $x^2=t,t \geq 0$

t^2-19t+34=0

t_1=2;t_2=17

Исходя из области определения корнями будут:

$x_1=-\sqrt{2};x_2=\sqrt{2};x_3=-\sqrt{17};x_4=\sqrt{17}$

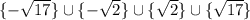
ответ: $\{-\sqrt{17}\}\cup\{-\sqrt{2}\}\cup\{\sqrt{2}\}\cup\{\sqrt{17}\}$

$\sqrt[4]{25x^2-144}=x$

Область определения уравнения:

$25x^2-144 \geq 0$

$x\in(-\infty;-\frac{12}{5}] \cup [\frac{12}{5};+\infty)$

Преобразовывая область определения отбросим левую часть,так как корень равен неотрицательному числу(в данном случае числом является x,и при отрицательных x равенство не имеет место)

$x\in[\frac{12}{5};+\infty)$

Возведем обе неотрицательные части в четвертую степень:

25x^2-144=x^4

x^4-25x^2+144=0

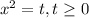
Решение подобного биквадратного уравнения сводится к замене вида: $x^2=t,t \geq 0$

t^2-25t+144=0

t_1=16;t_2=9

Исходя из области определения корнями будут:

x_1=3;x_2=4

ответ: $\{3\} \cup \{4\}$

0,0(0 оценок)

Популярные вопросы: Алгебра

Y563280

18.10.2022 07:41

Выражение и найдите его значение при x=1,5 x+1. x-1. x^2+1. x^2-1 ( - ) : ( - ) x-1. x+1. x^2-1. x^+1...

daniilkomarov

18.10.2022 07:41

Представьте в виде суммы разрядных слагаемых: а) 6,25 б)1,37 в)0,234 г)5,1351...

калькуляторлена

18.10.2022 07:41

Образующая конуса равна 4 см, наклонена к плоскости основания под углом 60 градусов.найдите площадь осевого сечения конуса....

radugraduga887

15.06.2021 17:58

Cos 11п/3 (одиннадцать пи делённая на 3) *умножить* ctg(-21п/4). вычислить при формул...

alinkamomot2004

15.06.2021 17:58

Записать число в виде суммы разрядных слагаемых: 0,15268...

glazyrinasasha

15.06.2021 17:58

Y= 3 x в четвертой степени -2\3 x в кубе + 3\5x+5 найти производную...

alikrufgffgfgf

15.06.2021 17:58

Проехал 560 км на поезде со скоростью 70 км/ч ,потом пешком 35 км со скорость 5 км/ч ,а затем проплыл на теплоходе 550 км со скоростью 22 км/ч. найдите среднюю скорость...

overmaker

15.06.2021 17:58

Периметр треугольника pм, а каждая из двух сторон равна 0,31p. а) найдите третью сторону этого треугольника...

SlavaKirja

15.06.2021 17:58

Найдите наибольшее и / или наименьшее значение функции: y=3x^2-24x-100. а) на отрезке [-1; 5]; б) на луче (- бесконечность; 0]...

илья20067

18.02.2020 03:38

Произошло наводнение на участке 500м2 и в течении 1 часа вода поднялась на 50 см. Какого скорость заполнения воды в м3 за 1 минуту ?...

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку