Стандартные решения через дискриминант уже написаны, можно по ним свериться. Предложу "быстрые", но которые не всегда срабатывают.
- видно, что сумма коэффициентов в этом квадратном уравнении равна 0. Корни находятся быстро и безболезненно.
ответ:
б) тут действительно проще всего выделить полный квадрат. С опытом приходит их видение.
ответ:
в)
Здесь или проще
В этом случае
ответ:
P.S. как видим, ни разу не был вычислен дискриминант. И примеров таких уравнений довольно много, в том числе и на экзаменах. Поэтому советую запомнить эти частные случаи и тренироваться побольше.
D=(-(-5))²-4×3×2=25-24=1
x1=(-(-5)+√1)/2×3=(5+1)/6=6/6=1
x2=(-(-5)-√1)/2×3=(5-1)/6=4/6=⅔
b) 4x²-4x+1=0
(2x-1)²=0
2x-1=0
2x=1|÷2
x=½.
Можно решить через дескриминант:
D=(-(-4))²-4×4×1=16-16=0
Так как D=0, то квадратное уравнение имеет один корень:
х=((-b)/2a)
х=((-(-4)/2×4))
х=4/8, сокращаем на 4
х=½.
c) 2x-x²+3=0
-x²+2x+3=0
D=(-2)²-4×3×(-1)=4+12=16
x1=(-2+√16)/2×(-1)=(-2+4)/(-2)=2/(-2)=-1
x2=(-2-√16)/2×(-2)=(-2-4)/(-2)=(-6)/(-2)=3
можно решить данное квадратное уравнение по теореме Виета:
х²+px+q=0
x1+x2=-p
x1×x2=q
-х²+2х+3=0|×(-1)
х²-2х-3=0
х1+х2=-(-2)=2
х1×х2=-3
х1=-1
х2=3
Стандартные решения через дискриминант уже написаны, можно по ним свериться. Предложу "быстрые", но которые не всегда срабатывают.
ответ: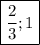
б) тут действительно проще всего выделить полный квадрат. С опытом приходит их видение.
ответ: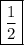
в)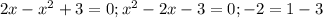
Здесь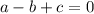 или проще
или проще 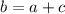
В этом случае
ответ: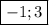
P.S. как видим, ни разу не был вычислен дискриминант. И примеров таких уравнений довольно много, в том числе и на экзаменах. Поэтому советую запомнить эти частные случаи и тренироваться побольше.