Алгебра꧁꧁꧁꧁꧁꧁} ₩꧁꧂꧂꧂꧂꧂꧂꧂​

В решении.

Объяснение:

В отеле Санкт-Петербурга есть 2-х местные и 3-х местные номера, в  которые заселили 27 гостей из Москвы таким образом, что гости заняли  10 номеров. Ночь в двухместном номере на одного человека стоит 2000  рублей, ночь в трёхместном номере на одного человека стоит 1500  рублей. Сколько рублей суммарно потратили все гости из Москвы за  одну ночь в отеле?

х - количество двухместных номеров.

у - количество трёхместных номеров.

1) По условию задачи система уравнений:

х + у = 10

2х + 3у = 27

Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:

х = 10 - у

2(10 - у) + 3у = 27

20 - 2у + 3у = 27

у = 7 - количество трёхместных номеров.

х = 10 - у

х = 3 - количество двухместных номеров.

2) Оплата:

3*2 = 6 (чел.) в двухместных номерах * 2000 = 12 000 (руб.);

7*3 = 21 (чел.) в трёхместных номерах * 1500 = 31 500 (руб.);

Суммарно: 12 000 + 31 500 = 43 500 (руб.).

Для решения запишем формулу бинома Ньютона:

Если а - слагаемое, содержащее неизвестную в наибольшей степени, то для определения степени результата нужно рассмотреть выражение .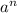

Если b - слагаемое, не содержащее неизвестную, то для определения свободного члена результата нужно рассмотреть выражение .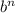

Рассмотрим многочлен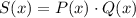 , где:

Для определения степени и свободного члена произведения достаточно знать степень и свободный член каждого из множителей.

Для многочлена :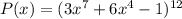

- степень определяется выражением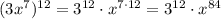 , то есть степень равна 84

- свободный член равен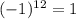

Для многочлена :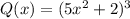

- степень определяется выражением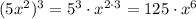 , то есть степень равна 6

- свободный член равен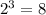

Наконец, для многочлена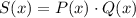 получим:

- степень определяется выражением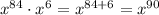 , то есть степень равна 90

- свободный член равен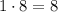

Сумма степени и свободного члена многочлена :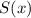

ответ: 98