Для того чтобы доказать, что множество не замкнуто, нам достаточно найти два иррациональных числа - сложить их и в результате получить рациональное число. То есть сумма двух иррациональных чисел не всегда иррациональна, то есть не замкнуто на иррациональности. Возьмем простейшее иррациональное число √2 и соответсвенно -√2 сложим √2 + (-√2) = √2 - √2 = 0 0 число рациональное . Тем самым мы нашли два иррациональных числа, которые при сложении дают рациональное число Так же доказывается незамкнутость иррациональных чисел при 1. разности 1+√3 и √3 равна 1 2. произведении √2 и 2√2 равно 4 3. делении 2√2 и √2 равно 2
Докажем что √2 иррациональное число Предположим что оно рациональное то есть его можно представить в виде несократимой дроби √2=a/b где a , целые и взаимнопросты (в противном случае они бы сократились) замечаем что a b оба не четные (если бы были оба четными то сократились на 2) Возводим в квадрат 2=a²/b² 2b²=a² замечаем что число 2b² четное, значит и a² тоже четное. заменяем a=2c и подставляем в 2b²=(2c)²=4c² b²=2c² получили что и b четное. То есть a b четные и их можно сократить, но мы предполагали что они взаимнопросты, и тем самым допустили противоречие. Значит √2 нельзя представить в виде дроби и оно иррациональное число
Возьмем простейшее иррациональное число √2 и соответсвенно -√2
сложим √2 + (-√2) = √2 - √2 = 0
0 число рациональное . Тем самым мы нашли два иррациональных числа, которые при сложении дают рациональное число
Так же доказывается незамкнутость иррациональных чисел при
1. разности 1+√3 и √3 равна 1
2. произведении √2 и 2√2 равно 4
3. делении 2√2 и √2 равно 2
Докажем что √2 иррациональное число
Предположим что оно рациональное то есть его можно представить в виде несократимой дроби √2=a/b где a , целые и взаимнопросты (в противном случае они бы сократились) замечаем что a b оба не четные (если бы были оба четными то сократились на 2)
Возводим в квадрат 2=a²/b² 2b²=a² замечаем что число 2b² четное, значит и a² тоже четное. заменяем a=2c и подставляем в 2b²=(2c)²=4c²
b²=2c² получили что и b четное. То есть a b четные и их можно сократить, но мы предполагали что они взаимнопросты, и тем самым допустили противоречие. Значит √2 нельзя представить в виде дроби и оно иррациональное число
(см. объяснение)
Объяснение:
Самый верный решить любой параметр - это постараться построить его в координатах (b; x).
Попробуем применить этот прием здесь.
Сначала заметим, что при
равенство неверно при любом значении параметра. Тогда на протяжении решения при необходимости будем спокойно делить на 
.
Раскроем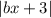
:
Видим гиперболу в координатах (b; x).
Построим ее и просчитаем знаки в областях, которые она образует, подставляя координаты соответствующих точек в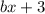
.
Тогда при
:
Строим фрагмент этого графика в определенных выше областях.
При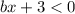
:
Тоже строим фрагмент этого графика в определенных выше областях.
Получим график уравнения:
(см. прикрепленный файл)
Итого:
ПриЗадание выполнено!