По формуле:
Замена переменной:
Возводим в квадрат:
⇒
Уравнение примет вид:
или
Обратный переход ( обратная замена):
не имеет корней, т.к
|sin2x|≤1 и |cos2x|≤1, а
наименьшее значение (-1)
они не могут принимать
одновременно
О т в е т.
4cos²x+4cos²x*sin2x-1=0
4cos²x(1+sin2x)-1=0
4cos²x(sin²x+2sinx*cosx+cos²x)-1=0
4cos²x(sinx+cosx)²-1=0
(2cosx(sinx+cosx)-1)(2cosx(sinx+cosx)+1)=0
1) 2cosx(sinx+cosx)-1=0
2cosx*sinx+2cos²x-1=0
sin2x+cos2х=0
делим на cos2х≠0. иначе бы и sin2x=0, но это не так.
tg2x=-1; 2x=-π/4+πm m∈Z;
x=-π/8+πm/2; m∈Z;
2) 2cosx(sinx+cosx)+1=0
2cosx*sinx+2cos²x+sin²x+cos²x=0
2cosx*sinx+3cos²x+sin²x=0
2tgx+3+tg²x=0 нет корней, т.к. дискриминант равен 4-12=-8 отрицателен.
По формуле:
Замена переменной:
Возводим в квадрат:
Уравнение примет вид:
Обратный переход ( обратная замена):
они не могут принимать
одновременно
О т в е т.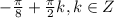
4cos²x+4cos²x*sin2x-1=0
4cos²x(1+sin2x)-1=0
4cos²x(sin²x+2sinx*cosx+cos²x)-1=0
4cos²x(sinx+cosx)²-1=0
(2cosx(sinx+cosx)-1)(2cosx(sinx+cosx)+1)=0
1) 2cosx(sinx+cosx)-1=0
2cosx*sinx+2cos²x-1=0
sin2x+cos2х=0
делим на cos2х≠0. иначе бы и sin2x=0, но это не так.
tg2x=-1; 2x=-π/4+πm m∈Z;
x=-π/8+πm/2; m∈Z;
2) 2cosx(sinx+cosx)+1=0
2cosx*sinx+2cos²x+sin²x+cos²x=0
2cosx*sinx+3cos²x+sin²x=0
2tgx+3+tg²x=0 нет корней, т.к. дискриминант равен 4-12=-8 отрицателен.