4. Запишите уравнение параболы, которую можно получить сдвигом параболы у = x² вдоль оси абсцисс на 4 единицы влево
и вдоль оси ординат на 2 единицы вверх
​

62. 7см, 14см, 10см

67. 7  девочек - в тренажерный зал

12 девочек - на шейпинг

14 девочек -на аквааэробику

69.

15 км/ч и 12 км/ч

62. Пусть х- меньшая сторона треугольника, тогда 2х- вторая сторона треугольника и (х+3)- третья сторона треугольника

х+2х+х+3=31 ;

4х=31-3;

х=28:4;

х=7( см)- 1 сторона

2х=2*7=14(см)- вторая сторона

х+3=7+3=10(см) - третья сторона

67.

Пусть в тренаженый зал ходит х старшекласниц, тогда (х+5) старшекласниц ходят на шейпинг и 2х- на аквааэробику.

По условию задачи составим уравнение:

х+х+5+2х=33;

4х=33-5;

х=28:4;

х=7 (ст.) - в тренажерный зал

х+5=7+5=12 (ст.) - на шейпинг

2*7=14 ( ст.) -на аквааэробику

69. Пусть х - скорость второго велосипедиста, а (х+3) - скорость первого. Тогда (х+х+3)- совместная скорость, с которой оба проехали путь до встречи за 40 минут

40минут=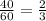 часа

18=(х+х+3)*2/3;

2х+3=18*3/2;

2х=27-3;

х=24:2;

х=12 (км/ч)- скорость второго велосипедиста

х+3=12+3=15(км/ч)- скорость первого велосипедиста

Ре­ше­ние.

С по­мо­щью фор­му­лы Ге­ро­на по­счи­та­ем пло­щадь дан­но­го тре­уголь­ни­ка. По­лу­пе­ри­метр равен

\rho= дробь, чис­ли­тель — 11 плюс 12 плюс 7, зна­ме­на­тель — 2 =15.

Тогда пло­щадь равна

S= ко­рень из { \rho(\rho минус 11)(\rho минус 12)(\rho минус 7)}= ко­рень из { 15 умно­жить на 4 умно­жить на 3 умно­жить на 8}=12 ко­рень из { 10}.

Далее най­дем вы­со­ту через пло­щадь и сто­ро­ну тре­уголь­ни­ка. Наи­мень­шая вы­со­та про­ве­де­на к наи­боль­шей сто­ро­не, по­это­му

h= дробь, чис­ли­тель — 2 умно­жить на S, зна­ме­на­тель — 12 = дробь, чис­ли­тель — 2 ко­рень из { 10}, зна­ме­на­тель — 7 .

Под­став­ляя зна­че­ние 3,16 вме­сто ко­рень из { 10}, по­лу­ча­ем:

h\approx 2 умно­жить на 3,16=6,32.

ответ: 6,32.