4. Прямоугольный участок площадью 4900 м’ огораживают забором. Каковы должны быть размеры участка, чтобы на забор ушло наименьшее количество материала? Решите задачу с производной. [5]
х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увели чилась вдвое, общий доход семьи вырос бы на 67% . Если бы стипендия дочери уменьшилась втрое, общий доход семьи со кратился бы на 4% . Сколько процентов от общего дохода семьи составляет зарплата жены? Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67% , то есть зарплата мужа составляет 66% дохода семьи. Если бы стипендия дочери уменьшилась втрое, общий доход семьи со кратился бы на 4% , то есть 2/3 стипендии составляют 6% дохода семьи, а вся стипен дия дочери составляет дохода семьи. Таким образом100%-67%-6%=27%, доход жены составляет дохода семьи. ответ : 27. извиняюсь, что с ошибками, просто с телефона)
y наиб = у max = 54
Объяснение:
Дана функция y= (27 - x) · √x
Производная этой функции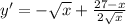
Упростим это выражение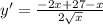
х ≠ 0 , но этот разрыв производной нас не интересует, поскольку мы ищем наибольшее значение в интервале [1; 16]
y' = 0
(27 - 3x) = 0
Точка экстремума одна x = 9.
При х < 9 y' > 0; при х > 9 y' < 0. Следовательно, точка х = 9 - точка максимума. И на концах интервала при непрерывной производной в заданном интервале значения функции будут меньше её значения в точке локального максимума.
у наиб = у max = y(9) = (27 - 9) · √ 9 = 54