Кусочная функция на графике нарисована сплошными линиями .
Рисуем параболу при изменении переменной "х" в пределах от -3 до 3 , . Ветви параболы направлены вверх, вершина параболы находится в точке (-1;-16) . Точки (3;0) и (-3;-12) принадлежат графику .
Прямую рисуем при . Точка (3;0) не принадлежит графику .
Прямую рисуем при . Точка (-3;-12) не принадле-жит графику .
А задачка-то хорошая! Сумма номеров - это сумма арифметической прогресс с разностью 2. Пишем по формуле суммы, вместо d ставим 2, приравниваем к 435. Сокращаем двойки, получаем а+n-1=435/n Раскладываем 435 на множители = 3*5*29. Причём по условию домов больше 8 и число 435/n должно быть целым. Значит имеем несколько вариантов: домов в квартале 15 или 29 или 3*29=87 или 5*29=145 Начинаем с 15: а+14=29 а=15, т. е. первый дом в квартале имеет номер 15, восьмой - 15+7*2=29. Остальные варианты дают отрицательное число и нас по этому не интересуют. Итак, ответ: 29. Как-то так.
Кусочная функция на графике нарисована сплошными линиями .
Рисуем параболу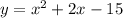 при изменении переменной "х" в пределах от -3 до 3 ,
при изменении переменной "х" в пределах от -3 до 3 , 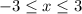 . Ветви параболы направлены вверх, вершина параболы находится в точке (-1;-16) . Точки (3;0) и (-3;-12) принадлежат графику .
. Ветви параболы направлены вверх, вершина параболы находится в точке (-1;-16) . Точки (3;0) и (-3;-12) принадлежат графику .
Прямую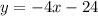 рисуем при
рисуем при 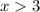 . Точка (3;0) не принадлежит графику .
. Точка (3;0) не принадлежит графику .
Прямую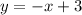 рисуем при
рисуем при 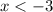 . Точка (-3;-12) не принадле-жит графику .
. Точка (-3;-12) не принадле-жит графику .
б) область значений функции: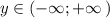 ,
,
при х=5 значение функции у=-2 ,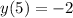 .
.
в) пересечение с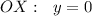 при
при 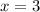 ,
, 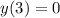 .
.
пересечение с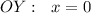 , если
, если 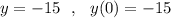 .
.
г) y(x) возрастает при![x\in [-1\ ;\ 3\ ]](/tpl/images/1787/8390/dc20e.png) .
.
y(x) убывает при![x\in (-\infty ;-1\ ]\cup [\ 3\ ;+\infty \, )](/tpl/images/1787/8390/485e8.png) ,
,
Сумма номеров - это сумма арифметической прогресс с разностью 2.
Пишем по формуле суммы, вместо d ставим 2, приравниваем к 435.
Сокращаем двойки, получаем
а+n-1=435/n
Раскладываем 435 на множители = 3*5*29. Причём по условию домов больше 8 и число 435/n должно быть целым.
Значит имеем несколько вариантов:
домов в квартале 15 или 29 или 3*29=87 или 5*29=145
Начинаем с 15:
а+14=29
а=15, т. е. первый дом в квартале имеет номер 15, восьмой - 15+7*2=29.
Остальные варианты дают отрицательное число и нас по этому не интересуют.
Итак, ответ: 29.
Как-то так.