3)РОЗВЯЖІТЬ СИСТЕМИ: а підстановки х+4у=-6 і 3х-у=8; б додавання 7х+3у=43 і 4х-3у=67; в)Графічним х+у=3 і 2х-у=3; (замість букв і має бути системна душка )
Сумма коэффициентов при четных (2) и нечетных (1+1=2) степенях равна, значит, x=-1 - корень.
Осталась последняя скобка в разложении, найдем дискриминант уравнения
при любых х.
Итоговое разложение
Нули производной известны, это
Везде при х коэффициент равен 1 (у правой скобки нет нулей, её мы считаем просто каким-то положительным числом), значит, в самом правом промежутке "+", а дальше чередование.
Имеем при возрастание , а при убывание ,
- точка локального максимума,
- точка локального минимума.
Убывание должно быть на интервале , поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.
С одной стороны, , как раз при убывание на выполняется.
С другой стороны, , при убывание продолжается вплоть до x=1, не включая эту точку.
Хорошо, вам не объяснили толково что такое вообще математическая логика, но это на самом деле нормальный случай, сами дают и не знают, что дают. Давайте разберемся. Пусть некоторое A - утверждение. Будем называть утверждением некоторое предположение, которое характеризуется либо как истинное и тогда утверждение равняется единице, либо как ложное и тогда утверждение равняется нулю. В данном случае за утверждение принимается: A - предположение, говорящее, что Первая буква гласная. B - предположение, говорящее, что Последняя буква согласная. Немного об операциях в т.н. алгебре логики (термин сложный и его нужно разъяснять отдельно, делается это в курсе т.н. "высшей алгебры"). Это сложение (известное также как объединение в теории множеств) и умножение (пересечение). Здесь их называют логическое "ИЛИ" (дизъюнкция) и логическое "И" (конъюнкция). Раз уж речь идет об алгебре, то, конечно, имеем также логическое "НЕ". По аналогии с теорией множеств, это дополнение к какому-то операнду (а суть унарная операция, интересная вещь). Давайте запишем как нужно само выражение. -A∧-B (вместо минусов нужно черточку над буквой). Таблица истинности выглядит так: В наименованиях столбцов пишите A и B и ваше выражение третьим. Затем подставляете различные наборы значение A и B, A и B принимают только значения 0 и 1. Получаете соответственно 0 или 1. "НЕ" - значит, утверждение обращается - было 1, стало 0, и наоборот. "И" - дает 1 если оба операнда 1, иначе дает 0. "ИЛИ" - дает 0 если оба операнда 0, иначе дает 1. Вот и все. Заполняете и получаете нужное.
Ну указывает на то, что надо бы производную брать для исследования этой функции, ибо она красивая получается.
указывает на то, что надо бы производную брать для исследования этой функции, ибо она красивая получается.
Далее, для исследования исходной функции на возрастание/убывание необходимо найти нули производной, то есть
Сумма коэффициентов в уравнении равно 0, значит, x=1 - корень
Попробуем разложить выражение, заранее зная корень.
Теперь нужно проанализировать правую скобку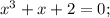
Сумма коэффициентов при четных (2) и нечетных (1+1=2) степенях равна, значит, x=-1 - корень.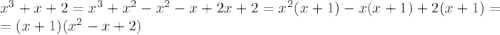
Осталась последняя скобка в разложении, найдем дискриминант уравнения
Итоговое разложение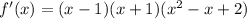
Нули производной известны, это
Везде при х коэффициент равен 1 (у правой скобки нет нулей, её мы считаем просто каким-то положительным числом), значит, в самом правом промежутке "+", а дальше чередование.
Имеем при возрастание
возрастание 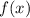 , а при
, а при 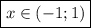 убывание
убывание 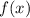 ,
,
Убывание должно быть на интервале , поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.
, поэтому если параметр захватит точки экстремума - ничего страшного, интервал как раз не включает концы.
С одной стороны, , как раз при
, как раз при  убывание на
убывание на 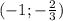 выполняется.
выполняется.
С другой стороны,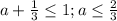 , при
, при  убывание продолжается вплоть до x=1, не включая эту точку.
убывание продолжается вплоть до x=1, не включая эту точку.
Объединяя наши условия, получаем![$1\leq a\leq \frac{2}{3} \Rightarrow a\in[1;\frac{2}{3}]](/tpl/images/0725/1569/fb3d8.png)
ответ:![\boxed {a\in[1;\frac{2}{3}]}](/tpl/images/0725/1569/80e87.png)
Давайте разберемся.
Пусть некоторое A - утверждение. Будем называть утверждением некоторое предположение, которое характеризуется либо как истинное и тогда утверждение равняется единице, либо как ложное и тогда утверждение равняется нулю.
В данном случае за утверждение принимается:
A - предположение, говорящее, что Первая буква гласная.
B - предположение, говорящее, что Последняя буква согласная.
Немного об операциях в т.н. алгебре логики (термин сложный и его нужно разъяснять отдельно, делается это в курсе т.н. "высшей алгебры").
Это сложение (известное также как объединение в теории множеств) и умножение (пересечение). Здесь их называют логическое "ИЛИ" (дизъюнкция) и логическое "И" (конъюнкция). Раз уж речь идет об алгебре, то, конечно, имеем также логическое "НЕ". По аналогии с теорией множеств, это дополнение к какому-то операнду (а суть унарная операция, интересная вещь).
Давайте запишем как нужно само выражение.
-A∧-B (вместо минусов нужно черточку над буквой).
Таблица истинности выглядит так:
В наименованиях столбцов пишите A и B и ваше выражение третьим.
Затем подставляете различные наборы значение A и B, A и B принимают только значения 0 и 1. Получаете соответственно 0 или 1.
"НЕ" - значит, утверждение обращается - было 1, стало 0, и наоборот.
"И" - дает 1 если оба операнда 1, иначе дает 0.
"ИЛИ" - дает 0 если оба операнда 0, иначе дает 1.
Вот и все. Заполняете и получаете нужное.