3. [ ) Представьте числа в виде уа и расположи их в порядке возрастания:
4√5.6√2;2√7;3√12
через 20 минут здавать

Показать ответ

Ответ:

dia49724zyf

12.09.2021 15:12

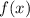Чтобы вычислить площадь фигуры, ограниченной графиком функции f(x) на заданном промежутке $[a; \ b]$ , следует найти определенный интеграл:

$\displaystyle \int\limits^b_a {f(x)} \, dx = F(x) |^{b}_{a} = F(b) - F(a),$

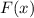где F(x) — первообразная для функции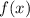 f(x)

1) Имеем функцию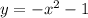 $y = -x^{2} - 1$ и следует вычислить площадь, которую она ограничивает на координатной плоскости на отрезке $[1; \ 2]$

Найдем определенный интеграл, приписав перед ним знак "минус", поскольку график функции находится под осью абсцисс:

$-\displaystyle \int\limits^2_1 {(-x^{2} - 1)} \, dx = \int\limits^2_1 {(x^{2} + 1)} \, dx = \left(\dfrac{x^{3}}{3} + x \right) \bigg| ^{2}_{1} = \dfrac{2^{3}}{3} + 2 - \left(\dfrac{1^{3}}{3} + 1 \right) = \dfrac{10}{3}$

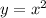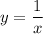2) Вычислим площадь фигуры, ограниченной графиками функций $y = x^{2}$ и $y = \dfrac{1}{x}$ на отрезке $[1; \ 3]$

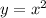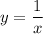Чтобы найти эту площадь, следует вычислить определенный интеграл разности функций $y = x^{2}$ и $y = \dfrac{1}{x}$ (только при такой разности площадей, образованных функциями на координатной плоскости, получим площадь фигуры, изображенной на рисунке):

$\displaystyle \int\limits^3_1 {\left(x^{2} - \dfrac{1}{x} \right)} \, dx = \left(\dfrac{x^{3}}{3} - \ln |x| \right)\bigg|^{3}_{1} = \dfrac{3^{3}}{3} - \ln 3 - \left(\dfrac{1^{3}}{3} - \ln 1 \right) = \dfrac{26}{3} - \ln 3$

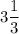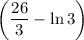ответ: 1) $3\dfrac{1}{3}$ кв. ед.; 2) $\left( \dfrac{26}{3} - \ln 3 \right)$ кв. ед.

0,0(0 оценок)

Ответ:

solovyovaolena

15.04.2022 04:28

Дано:

Правильная четырёхугольная пирамида FABCD.

S (основания) = 9 (см²).

FG = h = 12 (см).

Найти:

FH = ? (см).

Решение:

"В основании правильной четырёхугольной пирамиды лежит квадрат".

⇒ ABCD - квадрат. Чтобы найти сторону основания, нужно подобрать такое число, которое при возведении числа во 2 степень даёт ответ 9. Это число 3 ⇒ AB = BC = CD = DA = 3 (см).

Проведём из вершины F к стороне основания апофему FH, которая по свойству делит сторону основания пополам.

⇒ DH = HC = 3 : 2 = 1,5 (см).

Проведём из точки G к точке H отрезок. Внутри пирамиды образовался прямоугольный △FGH, где FG - катет прямоугольного треугольника (высота пирамиды), GH - катет прямоугольного треугольника, FH - гипотенуза прямоугольного треугольника (апофема пирамиды).

По свойству катет прямоугольного треугольника, который образован апофемой пирамиды, высотой и отрезком, их соединяющим, равен половине длины основания правильной четырёхугольной пирамиды.

⇒ DH = HC = GH = 1,5 (см).

Так как апофема FH является ещё и гипотенузой прямоугольного треугольника FGH, то найдём её по т.Пифагора (c = √(a² + b²), где c - гипотенуза, a и b - катеты).

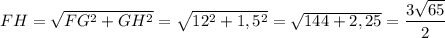$FH = \sqrt{FG^2+ GH^2} = \sqrt{12^2 + 1,5^2} = \sqrt{144 + 2,25} =\dfrac{3\sqrt{65}}{2}$ (см).

ответ: $\Large{\boxed{\dfrac{3\sqrt{65}}{2}}}$ (см).
В правильной четырёхугольной пирамиде площадь основания равна 9 см2, а высота пирамиды равна 12 см.