3. Определить для функции y=-5х3 и y = ax: 1) направление ветвей параболы; 2) промежутки возрастания и убывания функции; 3) координаты вершины параболы.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть , где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов:
Пусть х грн. - цена моркови; у грн. - цена лука.
{6х + 3у = 6,9
{4х + 5у = 7
- - - - - - - - - - -
Домножим обе части второго уравнения на 1,5
{6х + 3у = 6,9
{6х + 7,5у = 10,5
Вычтем из второго уравнения первое
4,5у = 3,6
у = 3,6 : 4,5
у = 0,8 (грн.) - цена лука
Подставим значение у в любое уравнение системы
6х + 3 · 0,8 = 6,9 или 4х + 5 · 0,8 = 7
6х + 2,4 = 6,9 4х + 4 = 7
6х = 6,9 - 2,4 4х = 7 - 4
6х = 4,5 4х = 3
х = 4,5 : 6 х = 3 : 4
х = 0,75 х = 0,75 (грн.) - цена моркови
Відповідь: 75 копійок ціна моркви; 80 копійок ціна цибулі.
210=2·3·5·7, поэтому число 210 имеет 4 простых делителя. Каждый делитель числа 210 может быть разложен на простые множители, то есть задается набором простых делителей, выбранных из множества простых делителей числа 210. Поэтому число делителей числа 210 равно числу подмножеств этого множества, то есть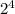
, где 4 - это сколько элементов в этом множестве (то есть его мощность). При этом единице соответствует пустое подмножество.
Остается найти вероятность по формуле, которая работает в случае, когда все элементарные исходы равновероятны: вероятность события равна отношению числа благоприятных исходов к общему числу исходов: