271. Составьте таблицу значений функции, заданной формулой у = х (х – 3,5), где 0 < x < 4, с шагом 0,5.
​

Понятно, что х - двузначное число. Пусть x=10a+b, где а, b - его цифры.
1) Если a+b - однозначное число, то его сумма цифр совпадает с ним и
х+у+z=(10a+b)+(a+b)+(a+b)=60, откуда 12а+3b=60, т.е. 4а+b=20. Возможны следующие варианты: a=5, b=0;  а=4, b=4. Если a<4, то  b>8 и тогда а+b не является однозначным.
2) Если а+b - двузначное, то его первая цифра равна 1, а вторая равна a+b-10, т.е. z=1+(a+b-10)=а+b-9. Итак,
x+y+z=(10a+b)+(a+b)+(a+b-9)=60, откуда 12а+3b=69, т.е. 4а+b=23.
Возможен только вариант а=4, b=7, т.к. .если a=5, то b=3 и a+b=8 - однозначное, а все остальные, очевидно, не подходят.
Значит итоговый ответ: число х может быть 50, 44 или 47.

 - красные

  - жёлтые

  - все шары

   все шары без одного, т.е. все оставшиеся.

По условию:      .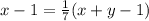

Получаем первое уравнение:

                   

Ещё по условию:   .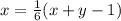

Второе уравнение:    

                       

Левые части обоих уравнений равны, значит, их правые части равны между собой.

                 

                 

                     красныx шаров в коробке.

Подставим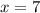    в уравнение  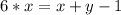   и получим:

                   

                 

                   

                      жёлтыx шаров в коробке.

         всего шаров в коробке.

ответ:     7  красныx;

               36  жёлтых;

                43 всего шаров в коробке.