20б. решение вероятностных с комбинаторики. 1. бросают две монеты - белую и желтую.найти вероятность того, что: 1) на обеих монетах появилась решка. 2. саша(с), варя(в) и гена(г) случайным образом заняли очередь в школьный буфет. найти вероятность того, что образовалась очередь в следующем
порядке: 1) свг 2) вгс 3) гсв или гвс 4) свг или всг 3. бросают два игральных тетраэдра- белый и зеленый, грани которых пронумерованы числами от 1 до 4. найти вероятность того, что появятся: 1) на белом тетраэдре 3 очка, на зеленом- 4 очка; 2)на белом тетраэдре 1 очко,на зеленом-2 очка; 3)на
белом тетраэдре четное число очков, на зеленом- 2 очка; 4) на белом тетраэдре нечетное число очков, на зеленом-3 очка 5)на белом тетраэдре 2 или 4 очка; 6) на зеленом тетраэдре 1 или 3 очка; 7)очки, сумма которых равна 2; 8) очки, сумма которых равна 8; 9) очки, сумма которых равна 7; 10)
очки, сумма которых равна 3; 11)очки, произведение которых равно 12; 12)очки, произведение которых равно 2; 13)очки, произведение которых равно 4; 14)очки, произведение которых равно 6;
Можно было сказать, что произведение и сумма состоят из двух чисел, если их можно поменять местами, то шанс —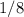 , иначе —
, иначе — 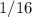 . То есть если мы говорим о произведении равном
. То есть если мы говорим о произведении равном  то если
то если 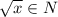 , если сумме — если
, если сумме — если