2 вариант

1.Выберите функции, графики которых параллельны, ответ обоснуйте: а. y=-3 и y=-3x+1 b. y= 1 - 5х и у=1+2х с. у= -6х+6 и у=-11x+11 d. y= -x+6 и у=-x+2 е. y=2,5х+4 и у= 1,5х+4

2.Определите, что является графиком функции y=5x”. Укажите график, соответствующий данной функции 11 4 Б 16 2

3.Установите соответствие между функциями и их графикални 1) y= 2х+3 2) y= x+4 3) y=x-4 4) y=2x-3 А Б В 3 A 3 1 E -2 -1 0 3 -2 A 1 -2 -1 0 А 2 г-2

4.Решите систем уравнений графическим : (3х + y = -1 1 х – у = 5

5.Найдите: а) области огре де іения функции. заданной формулой: 1) y= 2 – 3,7 x 2) y = 3х 6+х 3x +4 б) область значений рунки или у= , на отрезке 5

Задание: разложить на множители.
множители - компоненты при умножении ⇒выражение представляет собой произведение многочленов.
преобразовать данное выражение так, чтобы в каждом слагаемом были одинаковые множители.
1. m-n+p(m-n). 3-е слагаемое состоит из двух множителей р и (m-n), значит первое и  второе слагаемое группируем и записываем (m-n). необходимо представить в виде произведения двух множителей. один множитель (m-n), второй множитель в этом слагаемом может быть только 1. получаем:
m-n+p(m-n)=(m-n)*1+p*(m-n)=(m-n)*(1-p)

4q(p-1)+p-1=4q*(p-1)+(p-1)*1=(p-1)*(4q+1)

4q(p-1)+1-p=4q*(p-1)-1*(p-1)=(p-1)*(4q-1)

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t) - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение:

9t = 1

Значит,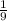 - цис./ч - производительность "медленного" насоса.

Тогда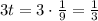 - цис./ч - производительность "быстрого" насоса.

Следовательно,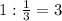 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.