2 Автомобиль начинает автомобиль начинает торможение с постоянным ускорением. Путь S (M), пройденный им за t секунд от начала торможения, вычисляется по формуле S = 30t – 5t^2 / 2
Определите время
от момента начала торможения, если известно, что за это время автомобиль проехал 80 метров.

Метод матем индукции
1) проверим делимость на 3 при n=1
при n=1 4n^3+6n^2+5n+9=4+6+5+9=24 - делится на 3
2) предположим что делится на 3 при n=k
при n=к 4n^3+6n^2+5n+9=4k^3+6k^2+5k+9=(3k^3+6k^2+3k+9)+(k^3+2k) - делится на 3
значит (k^3+2k) - делится на 3, так как (3k^3+6k^2+3k+9) делится на 3
3) проверим делимость на 3 при n=k+1
при n=к+1
4n^3+6n^2+5n+9=4(к+1)^3+6(к+1)^2+5(к+1)+9=
=(3(к+1)^3+6(к+1)^2+3(к+1)+9)+((к+1)^3+2(к+1)) = A+B
A=(3(к+1)^3+6(к+1)^2+3(к+1)+9) - делится на 3
B=(к+1)^3+2(к+1)=k^3+3k^2+3k+1+2k+2=(k^3+2k)+(3k^2+3k+3) = C+D
C = (k^3+2k) - делится на 3 (см пункт 2) )
D = (3k^2+3k+3) - делится на 3
значит B=C+D - делится на 3
значит 4n^3+6n^2+5n+9 при n=k+1 делится на 3
так как n=k+1 4n^3+6n^2+5n+9 = A+B
<<< доказано методом математической индукции >>>>

Правильное условие такое:

У брата х груш, а у сестры у² яблок. Вместе у них было 11 этих фруктов. Если бы у брата было у груш, а у сестры -х² яблок, то всего этих фруктов у них было бы 7. Сколько было груш и сколько было яблок? ​

Решение.

ОДЗ: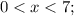    

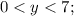
Методом подбора быстрее.

1) Начнем с решения второго уравнения.

Если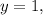 то 7-1=6. Тогда  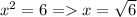не натуральное число.

Если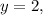 то 7-2=5. Тогда  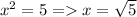не натуральное число.

Если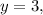 то 7-3=4. Тогда  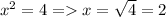натуральное число.

Получили решение

 

2) Подставим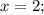 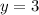     в первое уравнение   .

 

 

        верное равенство.

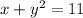ответ: 2 груши у брата;

           3 яблока у сестры.