Рассмотрим выражение . Чтобы оно было наименьшим, необходимо, чтобы выражения и были наименьшим.
Заметим, что выражение может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит, необходимо выбрать наименьшим, - наибольшим, - наименьшим.
Наибольшее . Наименьшие значения 2, 3, 4 нужно распределить между выражениями , и . Проверим все варианты.
Рассмотрим выражение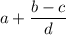 . Чтобы оно было наименьшим, необходимо, чтобы выражения
. Чтобы оно было наименьшим, необходимо, чтобы выражения  и
и 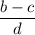 были наименьшим.
были наименьшим.
Заметим, что выражение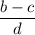 может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит,
может быть отрицательным. Если его числитель будет наименьшим отрицательным, а знаменатель - наименьшим положительным, то оно примет наименьшее значение. Значит, 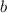 необходимо выбрать наименьшим,
необходимо выбрать наименьшим,  - наибольшим,
- наибольшим, 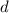 - наименьшим.
- наименьшим.
Наибольшее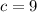 . Наименьшие значения 2, 3, 4 нужно распределить между выражениями
. Наименьшие значения 2, 3, 4 нужно распределить между выражениями  ,
, 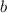 и
и 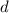 . Проверим все варианты.
. Проверим все варианты.
Пусть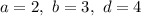 . Тогда:
. Тогда: 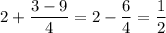
Пусть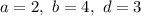 . Тогда:
. Тогда: 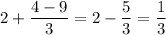
Пусть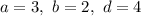 . Тогда:
. Тогда: 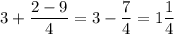
Пусть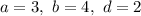 . Тогда:
. Тогда: 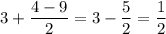
Пусть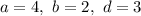 . Тогда:
. Тогда: 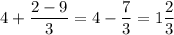
Пусть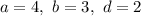 . Тогда:
. Тогда: 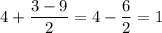
Наименьшее значение равно 1/3.
ответ: 1/3
Предполагая, что 0<a<90 , Определите 4(ctg²2α) , если sina=1/3.
* * * * * * * * * * * * * * * * * * * * * * * * * *
ответ: 6,125 .
Объяснение: * * *ctg(α+β) = (ctgα*ctgβ -1) / (ctgβ+ctgα) * * * || α=β ||⇒ ctg2α = (ctg²α -1) / 2ctgα.
4ctg²2α = 4*( (ctg²α -1 ) /2ctgα ) )² = (ctg²α -1 )²/ ctg²α
--- нужно вычислить (ctgα) ctg²α
ctg²α =cos²α /sin²α = (1 -sin²α) /sin²α =1 /sin²α - 1 =
sinα = 1/3 ⇒ sin²α = (1/3)² =1/9 , отсюда 1/sin²α = 9 и ctg²α = 8 .
Окончательно : 4ctg²2α = (ctg²α -1 )²/ ctg²α = (8 -1)²/8 = 49/8 = 6,125.
условие 0<a<90 оказалось лишнее (не был использован)