19. Суммы чисел строки треугольника Паскаля образуют интересную закономер- ность. Ее нетрудно обнаружить.
1. Используя рисунок 1, найди суммы чисел для каждой из первых шести
строк треугольника Паскаля. Заполни строку «Сумма в строке» таблицы:
Номер строки
Сумма
1
2
3
6.
4
5
Сумма в строке
2
Сумма В Виде
степени числа 2
21
2
2
2
2
2
2. Запиши найденные суммы в виде степени числа 2. Заполни строку «Сум-
ма в виде степени числа 2» таблицы.
3. Выяви закономерность: чему равна сумма чисел n-й строки треугольника
Паскаля.
Сумма чисел n-й строки треугольника Паскаля равна​

Объяснение:

Рассмотрим уравнение

t² - 4t + 5 = 0

D = 4² - 4*5 = 16 - 20 = -4

D = -4 < 0, следовательно уравнение не имеет действительных решений (график функции не пересекает ось Ох), график полностью находится в одной полуплоскости.

Рассмотрим значение коэффициента при старшей степени:

at² - bt + c

a = 1 > 0

Т.к. коэффициент при старшей степени положительный, ветви графика (парабола) направлена вверх.

График находится выше оси Ох, ветви направлены вверх, следовательно выражение t² - 4t + 5 при любом значении t принимает положительные значения

Переформулируем условие в терминах арифметической прогрессии:

1) В первый день потратили 100 рублей = первый член прогрессии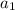 равен 100.

2) Каждый последующий день тратили на 50 рублей больше = разность прогрессии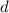 равна 50.

3) Всего было 1000 рублей = сумма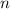 членов (то есть 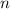дней) равна 1000.

Сумма вычисляется по формуле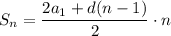

Чтобы найти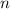 , подставим в эту формулу известные числа:

Решим это уравнение с дискриминанта:

Количество дней не может быть отрицательным, поэтому имеем единственный ответ: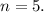

ответ: на пять дней.