Алгебра: 19.3. 1 и 3 19.4. 3 и 4

19.3. 1 и 3 19.4. 3 и 4

Показать ответ

Ответ:

aurantiuma

16.03.2023 05:50

Дан параллелограмм с диагоналями 80 и 120 см, разница его

сторон составляет 48 см. Примем меньшую сторону за х. Вторая будет х + 48.

Используем формулу диагоналей параллелограмма по теореме косинусов.

d1² = x² + (x + 48)² - 2*x*(x + 48)*cos B.

d2² = x² + (x + 48)² - 2*x*(x + 48)*cos D.

Во втором уравнении заменим cos D на -cos В по свойству углов параллелограмма.

d1² = x² + (x + 48)² - 2*x*(x + 48)*cos B.

d2² = x² + (x + 48)² +2*x*(x + 48)*cos В.

Подставим значения длин диагоналей и сложим уравнения.

80² + 120² = 2x² + 2(x + 48)².

6400 + 14400 = 2x² + 2(x + 48)².

20800 = 2x² + 2(x + 48)². Сократим на 2.

10400 = x² + (x + 48)². Раскроем скобки

10400 = x² + x² + 96x + 2304 или 2x² + 96x - 8096 = 0. Сократим на 2.

x² + 48x - 4048 = 0.

D=48^2-4*1*(-4048)=2304-4*(-4048)=2304-(-4*4048)=2304-(-16192)=2304+16192=18496;

Дискриминант больше 0, уравнение имеет 2 корня:

x_1=(2root18496-48)/(2*1)=(136-48)/2=88/2=44;

x_2=(-2root18496-48)/(2*1)=(-136-48)/2=-184/2=-92. Отрицательное значение отбрасываем.

Стороны равны 44 и 44+48 = 92 см.

ответ: периметр равен 2*(44+92) = 272 см.

0,0(0 оценок)

Ответ:

school91love

22.07.2022 00:50

1. Белоснежка из семи гномов может выбрать любых двух, любых трех, любых четверых, любых пятерых, любых шестерых или всех семерых. Двух гномов можно выбрать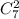 C_7^2 трех - 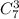C_7^3 и так далее до всех семи гномов, которых можно выбрать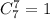 C_7^7=1

Тогда общее число можно рассчитать непосредственно как сумму:

C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7=C_7^2+C_7^3+C_7^3+C_7^2+C_7^1+C_7^0=

$=C_7^0+C_7^1+2C_7^2+2C_7^3=1+7+2\cdot\dfrac{7\cdot6}{1\cdot2} +2\cdot\dfrac{7\cdot6\cdot5}{1\cdot2\cdot3}=120$

Можно было воспользоваться интересным свойством для чисел сочетания:

C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7=

$=\left(C_7^0+C_7^1+C_7^2+C_7^3+C_7^4+C_7^5+C_7^6+C_7^7\right)-C_7^0-C_7^1=$

=2^7-C_7^0-C_7^1=128-1-7=120

ответ: 120

2. Рассмотрим ситуацию для слов длины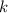 . Всего слов длины 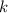можно составить 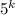5^k штук (или обозначая через размещения с повторениями 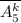$\overline{A_5^k}$ ). Слов длины 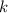, не содержащих букву "г", можно составить 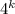4^k штук. Таким образом, слов длины 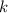, содержащих букву "г" можно составить $\left(5^k-4^k\right)$ штук.