На одном станке нужно обработать 90 деталей, а на другом - 100 деталей, причем на первом станке обрабатывается на 5 деталей в час больше, чем на втором. Сколько деталей в час обрабатывается на первом станке, если его работа была закончена на 1 час раньше, чем работа второго станка?
х - скорость обработки деталей на втором станке х + 5 - скорость обработки деталей на первом станке.
t - 1 - время работы первого станка t - время работы второго станка
х - скорость обработки деталей на втором станке
х + 5 - скорость обработки деталей на первом станке.
t - 1 - время работы первого станка
t - время работы второго станка
Тогда: { (x + 5)(t - 1) = 90
{ x*t = 100
{ t = 100/x
{ (x + 5)(100/x - 1) = 90
100 + 500/x - x - 5 - 90 = 0
5x + 500 - x² = 0
x² - 5x - 500 = 0 D = b²-4ac = 25+2000 = 2025 = 45²
x₁ = (-b+√D)/2a = (5+45):2 = 25 (дет./ч)
x₂ = (-b -√D)/2a = (5-45)/2 = -20 (не удовлетворяет условию)
х + 5 = 25+5 = 30 (дет./ч) - скорость обработки деталей на
первом станке.
ответ: 30 деталей в час.
Объяснение:
Первый модуль обращается в ноль при x=-2, второй - при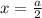 .
.
Пусть сначала
Тогда уравнение принимает вид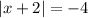 и, очевидно, не имеет решений.
и, очевидно, не имеет решений.
Пусть теперь
Если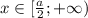 , то оба модуля раскрываются с плюсом и уравнение принимает вид:
, то оба модуля раскрываются с плюсом и уравнение принимает вид:
Полученный x будет корнем уравнения, если он принадлежит рассматриваемому отрезку, то есть если удовлетворяет системе неравенств
удовлетворяет системе неравенств
Решение системы: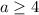
Если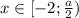 , то уравнение принимает вид
, то уравнение принимает вид
Полученный x будет корнем уравнения, если удовлетворяет системе:
удовлетворяет системе:
Решение системы: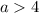
Пусть, наконец,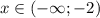 . Тогда уравнение принимает вид
. Тогда уравнение принимает вид
Полученный x будет корнем уравнения, если удовлетворяет системе:
удовлетворяет системе:
Эта система не имеет решений.
Теперь пусть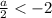 , то есть
, то есть 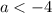 .
.
Если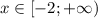 , то
, то
Система:
Нет решений.
Если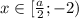 , то
, то
Система:
Решение системы: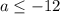
И наконец, если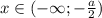 , то
, то
Система:
Решение: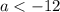
Из вышесказанного очевидно, что
При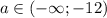 - два решения
- два решения
При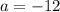 - одно решение
- одно решение
При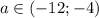 - нет решений
- нет решений
При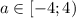 - нет решений
- нет решений
При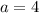 - одно решение
- одно решение
При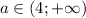 - два решения
- два решения
Таким образом, уравнение имеет одно решение при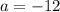 и
и