1.В лотерее из 100 билет(-ов, -а) 4 — счастливые.
Вычисли, какова вероятность того, что попадётся счастливый билет.
(пиши ответ в виде несокращённой дроби).
2.В лотерее из 970 билетов есть 4, каждый из которых «счастливый».
Вычисли вероятность того, что вынутый билет не будет «счастливым»!
(пиши ответ в виде несокращённой дроби).
3.На отдельных карточках написаны числа от 1 до 10, каждое 1 раз. Инна наугад вытаскивает две карточки. Какова вероятность того, что сумма чисел на вытащенных карточках будет равна 10?
(ответ вводи в виде сокращённой дроби.)
4.В комплекте игральных карт (колоде) — 52 карты. Наугад вытаскивается 1 карта. Вычисли вероятности событий:
(результат — несокращённая дробь, например, 36 записывай как «3/6»)
a) P(вытащенная карта является картой червовой масти) =
b) P(вытащенная карта является цифрой) =
c) P(вытащенная карта является дамой) =
d) P(вытащенная карта не является восьмёркой) =
e) P(вытащенная карта не является пиковой восьмёркой) =
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).
Объяснение:
Дана функция y=-x^2 + 6x - 5.
График этой функции - парабола ветвями вниз.
Вершина параболы Хо = -в/2а = -6/-2 = 3,
Уо = -9+18-5 = 4.
Точки пересечения оси Ох:
-х² + 6х - 5 = 0,
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=6^2-4*(-1)*(-5)=36-4*(-1)*(-5)=36-(-4)*(-5)=36-(-4*(-5))=36-(-(-4*5))=36-(-(-20))=36-20=16;Дискриминант больше 0, уравнение имеет 2 корня:
x₁=(√16-6)/(2*(-1))=(4-6)/(2*(-1))=-2/(2*(-1))=-2/(-2)=-(-2/2)=-(-1)=1;x₂=(-√16-6)/(2*(-1))=(-4-6)/(2*(-1))=-10/(2*(-1))=-10/(-2)=-(-10/2)=-(-5)=5.Точка пересечения оси Оу берётся из уравнения при х = 0, у = -5.
По графику (и по анализу) определяем:
1) промежуток убывания функции: х ∈ (3; ∞);
2) при каких значениях x функция принимает отрицательные значения:
х ∈ (-∞; 1) ∪ (5; +∞).
Всего три пары -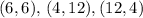
Объяснение:
Для того чтобы решить задачу, нужно правильно сформулировать проблему -
"Требуется найти все пары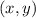
, где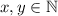 
так что 
."
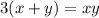Из равенства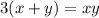
очевидно что 
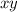делится на 3. Следовательно хотя бы одно из чисел 
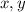делится на 3. Без огранчения общности, предположим что 
.
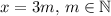Следовательно, высшеупомянотое равенство преообразовывается в
Заметим что отсюда выходит что,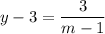
.
Т.к.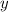
цело только и только тогда, когда 
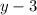цело, то следовательно, 3 должно делится на 
.
Число 3 делится только на четыре числа - 3, -3, 1, -1. Но лишь только два из них подходят - 3 и 1.
Следовательно,
Т.е.,
Отсюда получаем две пары -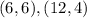
. Однако очевидно, что также и пара 
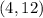подходит.