1. В числовом наборе 9 чисел, их среднее арифметическое равно 6. К этому набору добавили еще одно число x. Найдите среднее арифметическое чисел получившегося набора, если: а) x = 6 ; б) x = 12. Без вычислений определите, увеличится или уменьшится среднее арифметическое в каждом случае.

2. В первом наборе 8 чисел, их среднее равно 3. Во втором наборе 12 чисел, их среднее равно 5. Наборы объединили в один набор. Найдите среднее арифметическое нового набора.

Важно! Среднее арифметическое объединенного набора расположено на числовой прямой между средними двух исходных наборов. Так получилось не случайно.

3. В числовом наборе наименьшее значение равно 2, а наибольшее равно 9. Может ли среднее арифметическое такого набора быть равно: а) 6; б) 5 1/3; в) 1; г) 9? Если может, приведите пример такого набора, если нет, – объясните, почему.

4. В числовом наборе 23 числа. Одно (какое-то) из чисел этого набора увеличили на 1. Как и на сколько изменилось среднее арифметическое этого набора?

5. Вычислите среднее арифметическое чисел: а) 1, 2, 3, 4, 5; б) 1, 2, 3, 4, 10; в) 1, 2, 3, 4, 100;
г) 1, 2, 3, 4, 1000.

6. Вычислите среднее арифметическое двух числовых наборов 2, 4, 7, 8, 9 и 20, 40, 70, 80, 90.

Показать ответ

Ответ:

Флов227монстр

06.12.2022 08:33

Зависимость "двузначному числу ставится в соответствие сумма его цифр" является функциональной, так как каждое двузначное число имеет ровно одну сумму своих цифр.

Найдем требуемые значения:

f (12)=1+2=3

f (35)=3+5=8

f (92)=9+2=11

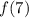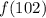Значения f(7) и f(102) найти невозможно, так как зависимость сформулирована лишь для двузначных чисел.

Область определения опять же вытекает из сформулированной зависимости: это все двузначные числа. Записать это можно так:

$D(f)=\{x\ |\ x\in\mathbb{N},\ 10\leqslant x\leqslant 99\}$

Найдем область значений. Во-первых, отметим, что сумма цифр двузначного числа по смыслу - это натуральное число. Далее, минимальную сумму цифр среди двузначных чисел имеет число 10 (сумма равна 1), а максимальную - число 99 (сумма равна 18). Можно показать, что все без исключения суммы от 1 до 18 могут быть получены на примере цепочки чисел:

10, 11, 12, ..., 18, 19, 29, 39, ..., 89, 99.

Таким образом, область значений:

$E(f)=\{x\ |\ x\in\mathbb{N},\ 1\leqslant x\leqslant 18\}$

0,0(0 оценок)

Ответ:

uefip

14.09.2021 11:45

Может быть так?

Два фермера, работая вместе, могут вспахать поле за 25 часов.
Производительность труда у первого и второго относятся как 2:5.
Фермеры планируют работать поочередно.
Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?

Пусть Х-производительность 1-го, У-производительность 2-го.
Система:

х+у=125
2х=5у
Последовательно:
2х+2у=2/25
2х-5у=0
7у=2/25 и у=2175
Тогда х=135
Итак, производительности мы нашли.
Поочередно фермеры работали 45,5 часа = 91/2 часа.
Пусть из этого времени 2-ой работал Т часов, тогда 1-ый работал 912-Т часов.
Уравнение:
(91/2-Т)⋅(1/35)+Т⋅(2/175)=1
имеет корень Т=17,5
Проверка.
1. проверим , что х+у=125
1/35+2/175=(70+175)/(175⋅35)=7/175=1/25
2. проверим, что 2х=3у:
2/35=5⋅2/175
3. Проверим уравнение при поочередной работе:
Если 2-ой работал 17,5 часов, то 1-ый работал 45,5-17,5=28 часов
28⋅135+(352)⋅(2175)=28/35+1/5=1
ОТВЕТ: 17,5