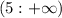1)у числа abc поменяли местами цифры b и c, сложили новое число с исходным и получили 787. найдите все такие числа abc. объясните, почему нет других.
2) у николая столько же сестёр, сколько и братьев. у его сестры вдвое меньше сестёр, чем братьев. сколько в этой семье мальчиков и сколько девочек?
3) страницы учебника пронумерованы числами от 1 до 368. хулиган джордж вырвал из разных мест учебника 15 листов, сложил номера всех вырванных страниц. у него получилось число 2020. возможно ли это?
все с объяснением,

Примем расстояние второго дня за х.

Тогда в первый день велосипедист проехал 

х+5 км

В третий день он проехал 3/7 от расстояния, пройденного за 2 первых дня, это 

3/7(х+х+5)=3/7(2х+5)

Всего велосипедист проехал 

2х+5+³/₇·(2х+5)=110     км. Это уравнение к задаче. 

2х+5+(6х+15):7=110 Умножим на 7, чтобы избавиться от дроби.

14х+35+6х+15=770

20х=720

х=36 км - проехал во второй день

36+5=41 проехал в первый день

36+41=77 проехал за 2 дня

³/₇·77=33 проехал за 3-й день

всего (проверка)

36+41+33=110 км

а)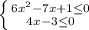

Строим координатную прямую и отмечаем на ней закрашенными точками 1\6 и 1

Получается, что х принадлежит [1\6;1]

Снова строим координатную прямую и отмечаем на неё закрашенную точку 3\4. Получаем, что х принадлежит

3) Общий

Отмечаем на координатной прямой все точки 1\6, 3\4 и 1.

Совмещаем графики и получаем решение системы уравнений.  

x принадлежит [1\6;\3\4]

Напоминаю, что вид скобок имеет значение.

б)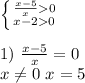

Строим координатную прямую и отмечаем на ней выколотые точки 0 и 5. х принадлежит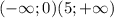

2) х>2

Строем координатную прямую с выколотой точкой 2 и получаем, что х принадлежит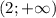

Объединяем значения на координатной прямой и получаем решение системы уравнений. х принадлежит