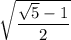1. составьте уравнение второй степени, один из корней которого был бы равен сумме, а второй – произведению корней уравнения х2 – 3х – 10 = 0. 2. найдите значение а, при котором уравнение (2а – 5) х2 – 2(а – 1) х + 3 = 0 имеет равные корни? 3. при всех значениях параметра а решите уравнение: а) х2
– 5ах +6а2 = 0, б) х2 + (а – 1) х – а = 0, в) х2 + (1 – 5а) х + 4а2 – а = 0, г) (2а – 2) х2 + (а + 1) х + 1 = 0. 4. при каком значении параметра а сумма квадратов корней уравнения х2 + (а – 1) х – а2 – 1,5 = 0 наибольшая? найдите её.

Если ты не умеешь применять теорему виета, то пиши в комментарях, я научу x²-8x+7 > 0 (х-1)(х-7) > 0 х € (-∞ ; 1 )( 7 ; +∞) x²+3x-54 < 0 (х+9)(х-6) < 0 х € ( -9 ; 6 ) 1/2x²+0,5x-1 > 0 x²+ x – 2 > 0 (х-1)(х+2) > 0 х € (-∞ ; -2 )( 1 ; +∞) 5x²+ 9,5x-1 < 0 10х²+19х–2 < 0 (х-1/10)(х+20/10)< 0 х € (-2 ; 0,1 ) -x²-3x+4> 0 x²+3x–4> 0 (х+4)(х-1)> 0 х € (-∞ ; -4 )( 1 ; +∞) -8x²+17x-2 ≤ 0 8x²-17x+2 ≤ 0 (х-16)(х-1) ≤ 0 х € [ 1 ; 16 ] дальше лень печатать (-∞ ; 3 )( 3 ; +∞) -12 нет корней (-∞ ; +∞) (-∞ ; 0,5 )( 0,5 ; +∞) нет корней

1.

ОДЗ: арксинус определен при

Найдем синус левой и правой части:

Уравнение распадается на два. Для первого уравнения получим:

Решаем второе уравнение:

Таким образом, уравнение имеет единственный корень 0.

ответ: 0

2.

ОДЗ: арксинус определен при

Найдем синус левой и правой части:

Так как в правой части стоит положительная величина, то и левая часть должна быть положительной, то есть .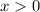

Возведем в квадрат обе части:

Решим биквадратное уравнение:

Находим х:

Однако, так как было выявлено ограничение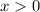 , то отрицательный корень не попадает в ответ.

Оценив значение полученного корня, мы понимаем, что он удовлетворяет исходной ОДЗ:

ответ: