1.
Реши неравенство при всех значениях параметра:
x/a>9.
(Бесконечность вводи как +Б или −Б.)
ответ:
если a>0, то x∈(..;..).
Если a=.., то нет решения.
Если a<0, то x∈(..;..).
2.
Определи, при каких значениях параметра m неравенство верно при любом действительном значении x:
x^2+9x+m>7.
ответ:
неравенство верно при любом действительном значении x , если m∈(..;+∞).
104.
a) cos 120 =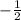
б) sin(-150)= -sin 150=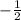
в) tg(-225)= -tg 225 = -1
г) cos(-225)=cos 225=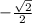
д) cos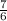
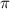 = cos 630 = 0
= cos 630 = 0
е)sin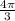 = sin 240 =
= sin 240 =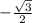
106.
а) sin ( -
-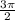 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-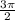 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2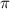 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 
Объяснение:
104.
cos(-α)= cos α
sin(-α)= -sin α
tg(-α)= -tg α
ctg(-α)= -ctg α
a) cos 120 =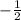
б) sin(-150)= -sin 150=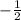 ( т.к. sin непарная функция => sin(-α)= -sin α )
( т.к. sin непарная функция => sin(-α)= -sin α )
в) tg(-225)= -tg 225 = -1 ( т.к. tg непарная функция => tg(-α)= -tg α )
г) cos(-225)=cos 225=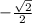 ( т.к. cos парная функция => cos(-α)= cos α )
( т.к. cos парная функция => cos(-α)= cos α )
д) cos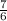
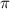 =
= 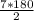 =630, 630=360+270 ( 360 это один полный оборот)
=630, 630=360+270 ( 360 это один полный оборот)
=> cos 270 cos 270 = 0
е)sin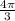 = sin 240 =
= sin 240 =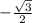
106.
В этом номере я использовал формулы приведения
их можно найти в интернете
а) sin ( -
-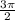 ) = sin (
) = sin ( -270) = sin (270-
-270) = sin (270- ) = -cos
) = -cos 
б) cos ( -
-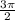 )= cos (
)= cos ( -270) = cos (270-
-270) = cos (270- ) = -sin
) = -sin 
в) tg ( -2
-2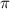 ) = tg (
) = tg ( -360) = tg (360-
-360) = tg (360- ) = -tg
) = -tg 
Объяснение:
1
(c-3)(c+3)+9=(c²+3c-3c-9)+9=c²+3z-3z-9+9=c²
Первый пропуск: с²
Второй пропуск: 9
Третий пропуск: с²
В первом задании появляется какое-то "+3z-3z" не переживаем это в сумме даёт ноль поэтому ничего страшного.Выражение в скобках "+3с-3с" также даёт ноль в сумме.Остаётся с²-9+9 (если прибавить к этому выражению "+3z-3z" от этого ничего не изменится т.к "+3z-3z" равно нулю... Считается что мы прибавили ноль, а любое выражение к которому прибавили ноль не изменит свой состав.-9 и +9 в сумме также дают нольответ: с² (третий пропуск)2
(b+4)(b-2)-2b=b²-2b+4b-8-2b=b²-4b+4b-8=b²-8
-4b+4b=0Самый последний пропуск: b²-8