1. Назовите верное высказывание *

1) Если a>b, то b 2) Если a>0, то a/3 > a/2
3) Если b 4) Если -×>1, то ×>-1
2. Даны два неравенства а) (×-3)(×+1)>(×-1)^2 б) x^2+2×+1×≥4× Назовите неравенства, верные при любых значениях x. *

1) а, б
2) а
3) б
4) нет верного ответа
3. Известно,что 4 ≤ a ≤ 5, 2 ≤ b ≤ 3. Оцените границы выражения 2a-b. В ответе укажите сумму целых значений выражения 2a-b, принадлежащим границам этого выражения. *

1) 13
2) 26
3) 20
4) 21
4. Округлите число до единиц и найдите относительную погрешность округления 8,536 *

1) 8%
2) 6,7%
3) 10%
5. Приближенное значение числа x равно a. Найдите абсолютную погрешность приближения, если x=2.76 a=2.8 *

1) 0,4
2) 0,04
3) 2

для определения среднего дохода налогоплательщиков города налоговой инспекцией была проведена проверка 250 жителей этого города, отобранных случайным образом. оценить вероятность того, что средний годовой доход жителей города отклонится от среднего арифметического    годовых доходов выбранных 250 жителей не более чем на 1000 руб., если известно, что среднее квадратичное отклонение годового дохода не превышает 2500 руб.

решение. согласно неравенству чебышева, которым можно пользоваться, поскольку все    , получаем

  .

теорема бернулли.  если в каждом из  п  независимых опытов вероятность  р  появления события  а  постоянна, то при достаточно большом числе испытаний вероятность того, что модуль отклонения относительной частоты появлений  а  в  п  опытах от  р  будет сколь угодно малым, как угодно близка к 1:

  .

замечание.  из теоремы бернулли не следует, что    . речь идет лишь о вероятности того, что разность относительной частоты и вероятности по модулю может стать сколь угодно малой. разница заключается в следующем: при обычной сходимости, рассматриваемой в анализе, для всех  п, начиная с некоторого значения, неравенство    выполняется всегда; в нашем случае могут найтись такие значения  п, при которых это неравенство неверно. этот вид сходимости называют сходимостью по вероятности.

Примем за 1 - объем цистерны

Пусть t цис./ч - производительность "медленного" насоса.

Тогда 3t цис./ч - производительность "быстрого" насоса.

(t+3t) цис./ч - производительность системы при совместной работе этих двух насосов.

(t+3t) - объем работы системы из двух насосов за 2ч 15мин.

Получим уравнение:

9t = 1

Значит,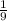 - цис./ч - производительность "медленного" насоса.

Тогда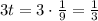 - цис./ч - производительность "быстрого" насоса.

Следовательно,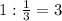 ч - потребуется "быстрому" насосу на заполнение цистерны.

ответ: 3 ч.