1)
Область определения функции: множество всех действительных чисел, т.е.
2)
В левой части неравенства свернем под формулу косинуса суммы аргументов
Далее на окружности смотрим (на фото)...
1)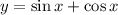
Область определения функции: множество всех действительных чисел, т.е.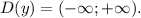
2)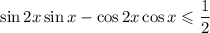
В левой части неравенства свернем под формулу косинуса суммы аргументов
Далее на окружности смотрим (на фото)...