1.на столе лежит 101 кучка по 101 спичке. за один ход берется одна спичка из любой кучки. двое игроков ходят по очереди. если не позднее 1-го хода будет взята последняя спичка из какой-то кучки, взявший её выигрывает, иначе — ничья. может ли кто-то из игроков выиграть независимо от игры соперника, и если да, то кто?
2. учитель написал на доске 10 отрицательных целых чисел. вася переписал в тетрадь эти числа, затем записал туда же всевозможные их попарные произведения, всевозможные произведения трёх, четырёх, …, девяти из этих чисел и, наконец, произведение всех десяти чисел. оказалось, что сумма всех записанных васей чисел отрицательна. чему она могла быть равна?

1) Заметим, что, если в кучке осталось 2 спички, никому из игроков не выгодно брать из нее спичку, т.к. следующим ходом противник заберет оставшуюся спичку и победит. Тогда, если есть кучка с 1 спичкой, забираем спичку, если же есть спички числом спичек, большим 2, берем спичку из любой.

Если во всех кучках осталось по 2 спички, то было совершено 99*101=9999 ходов, а значит последнюю спичку в данный момент забрал начинающий. Тогда на 10000 ход второй вынужден забрать спичку из кучки с 2 спичками. А дальше игра оканчивается ничьей.

А значит ответ нет.

2) Заметим, что искомая сумма .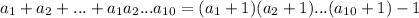

И правда. Пусть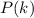 - сумма всех комбинаций по 1 ... по k элементов. Тогда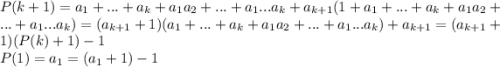

Т.к. числа отрицательны, то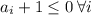

Если хотя бы одно из , вся сумма равна -1.

В остальных случаях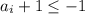 - всегда отрицательное. Но произведение 10 целых отрицательных чисел положительно, причем не меньше 1. Противоречие с тем, что .

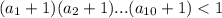А тогда сумма могла равняться только -1