1. 2/3•(3/4-10,5) ? 2. разложите на множители: 2x^2-3x-5=0 ? 3. составьте квадратное с заданных корней: (-4; 3) ? 4. решите уравнение: 2x^2+7-9=0 ? 5. решите неравенство: (x+3,7x) (7-x)> 0 ? 6. {x^2-5x-6< 0 ? {x-3》0 7. в6-? если в1=5; q=-2.? 8. из данных чисел выберите наибольшие: 1/2; 1/10; 0,018; 0,17; 0,49. ? 9. (15 1/5 -17): (-9)-3 1/4= ? 10. (3m-2) (3m+2)=5m^2 ? =_=_=_=_=_÷_÷_$_$_%_%-% $-$

Показать ответ

Ответ:

VaneK12354

19.08.2021 01:28

поскольку при каждом броске возможны только 2 исхода (орел или решка), то при 9 бросках возможны 2⁹ исходов. Из них количество исходов ровно с 5 выпадениями орла равно 9!/[5!(9-5)!], следовательно вероятность выпадения орла ровно 5 раз равна {9!/[5!(9-5)!]}/2⁹

Повторив аналогичные рассуждения, получим вероятность выпадения орла ровно 2 раза {9!/[2!(9-2)!]}/2⁹

найдем их отношение [{9!/[5!(9-5)!]}/2⁹]/[{9!/[2!(9-2)!]}/2⁹]=[2!(9-2)!]/[5!(9-5)!]= (1*2*1*2*3*4*5*6*7)/(1*2*3*4*5*1*2*3*4)=(6*7)/(3*4)=3.5

вероятность выпадения орлов ровно 5 раз в 3,5 раза выше, чем вероятность выпадения ровно 2 раза

0,0(0 оценок)

Ответ:

КРИЛЛ2000

07.08.2021 19:07

Формула работы: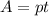 A=pt , р - производительность , t- время .

Если 6 насосов выкачивают воду из 1 бассейна за 10 часов, то за 1 час эти 6 насосов выкачают 1/10 часть бассейна. То есть производительность 6-ти насосов = 1/10 бассейна в час.

Производительность же 1 насоса равна (1/10):6=1/60 бассейна в час.

а) За 5 часов всю воду из 1 бассейна выкачают n насосов, то есть можно записать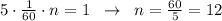 $5\cdot \frac{1}{60}\cdot n=1\; \; \to \; \; n=\frac{60}{5}=12$ насосов.

За 15 часов всю воду из 1 бассейна выкачивают m насосов, то есть можно записать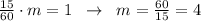 $\frac{15}{60}\cdot m=1\; \; \to \; \; m=\frac{60}{15}=4$ насоса.

б) Три насоса за 1 час выкачивают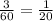 $\frac{3}{60}=\frac{1}{20}$ часть бассейна, значит всю воду из 1 бассейна три насоса выкачают за 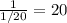$\frac{1}{1/20}=20$ часов.

9 насосов за 1 час выкачивают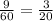 $\frac{9}{60}=\frac{3}{20}$ часть бассейна, значит всю воду из 1 бассейна 9 насосов выкачают за 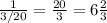$\frac{1}{3/20}=\frac{20}{3}=6\frac{2}{3}$ часa.